01.2 范式的演化

1.2 范式的演化⚓︎

在很多人眼里，AI来势汹汹，看样子会颠覆很多领域，这些新技术的出现有规律可循么？还会有什么别的技术突然出现让我们措手不及？这当然是有规律可循的。人类一直在试图了解客观规律，这种科学历史上发生了几次颠覆性的改变（范式转换）呢？我们通过Jim Gray的著作 $^{[5]}$ 可以看到，现在谈论的AI大潮就是属于data exploration这个范式转换的一部分。图1-8是Jim Gray著作中的插图，概述了范式演化的几个阶段，接下来我们将一一进行介绍。

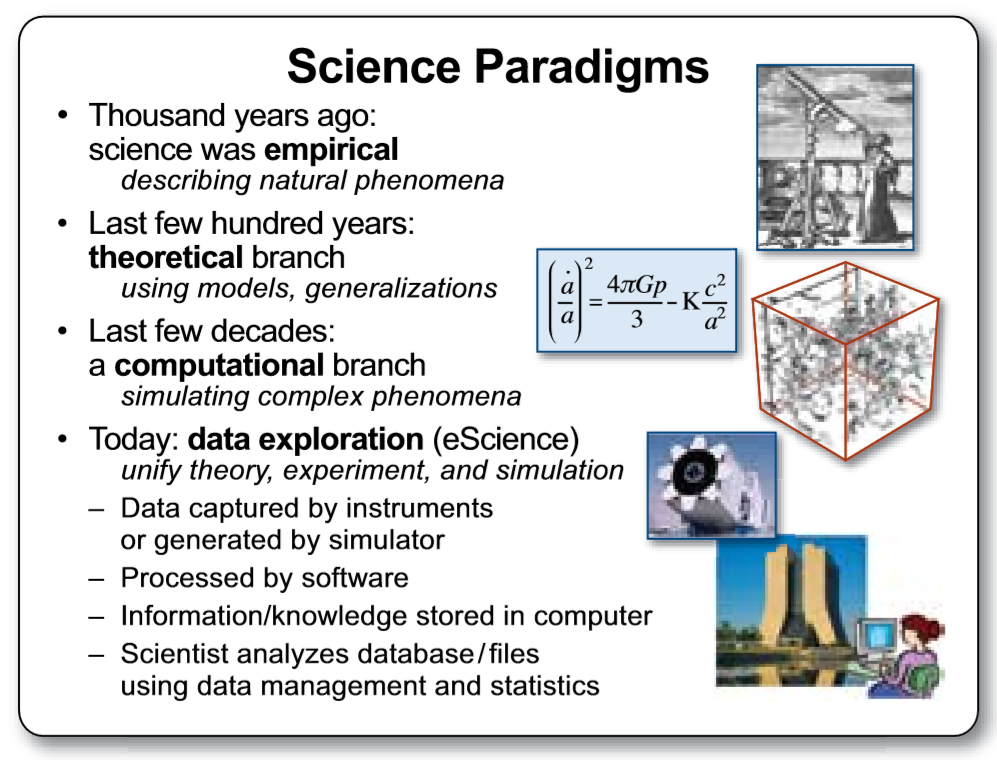
图1-8 Jim Gray著作中总结的范式演化的几个阶段

1.2.1 范式演化的四个阶段⚓︎

第一阶段：经验⚓︎

从几千年前到几百年前，人们描述自然现象，归纳总结一些规律。

人类最早的科学研究，主要以记录和描述自然现象为特征，不妨称之为称为“经验归纳”（第一范式）。人们看到自然现象，凭着自己的体验总结一些规律，并把规律推广到其他领域。这些规律通常是定性的，不是定量的。有时看似符合直觉，其实原理是错误的；有时在某个局部有效，但是推广到其他领域则不能适用；有些论断来自权威，导致错误总结也流传了很多年无人挑战。例如，我们看到日月星辰都围绕我们转，地心说很自然就产生了；我们在生活中观察不同质量的物体运动的情况，也凭直觉推断“物体的下落速度和重量成正比”。人们对于不同的观点，也没有严谨地定义试验来证明。例如中国古代“两小儿辩日”的故事：

孔子东游，见两小儿辩日，问其故。

一儿曰：“我以日始出时去人近，而日中时远也。”

一儿以日初出远，而日中时近也。

一儿曰：“日初出大如车盖，及日中则如盘盂，此不为远者小而近者大乎？”

一儿曰：“日初出沧沧凉凉，及其日中如探汤，此不为近者热而远者凉乎？”

孔子不能决也。

两小儿笑曰：“孰为汝多知乎？”

两个小孩通过视觉效果和身体对温度的感觉来判断太阳和地球的距离变化，而且小孩子们把主观的“我觉得它远”完全等同于“物体离我远”这样一个客观事实。这是一个多么大胆的思维跳跃啊，孔子当时也没有能设计一个试验来证伪某一个观点，只能诚实地表示“不能决”，还遭到小孩笑话。

第二阶段：理论⚓︎

这一阶段，科学家们开始明确定义，速度是什么，质量是什么，化学元素是什么（不再是五行和燃素）……也开始构建各种模型，在模型中尽量撇除次要和无关因素，例如我们在中学的物理实验中，要假设“斜面足够光滑，无摩擦力”，“空气阻力可以忽略不计”，等等。在这个理论演算（Theoretical）阶段，以伽利略为代表的科学家，开启了现代科学之门。他在比萨斜塔做的试验（图1-9）推翻了两千多年来大家想当然的“定律”。

图1-9 伽利略在比萨斜塔做试验

在理论演算阶段，不但要定性，而且要定量，要通过数学公式严格的推导得到结论。我们现在知道真空中自由落体下落的公式：

$h = \frac{1}{2}gt^{2}$

$h$ 是下落的高度， $g$ 是重力加速度， $t$ 是运动时间。

这个公式里没有物体的质量，所以我们可以说，在真空中，自由落体下落的速度的确和物体的质量无关。

第三阶段：计算仿真⚓︎

从二十世纪中期开始，利用电子计算机对科学实验进行模拟仿真的模式得到迅速普及，人们可以对复杂现象通过模拟仿真，推演更复杂的现象，典型案例如模拟核试验、天气预报等。这样计算机仿真越来越多地取代实验，逐渐成为科研的常规方法。科学家先定义问题，确认假设，再利用数据进行分析和验证。

第四阶段：数据探索⚓︎

最后我们到了“数据探索”（Data Exploration）阶段。在这个阶段，科学家收集数据，分析数据，探索新的规律。在深度学习的浪潮中出现的许多结果就是基于海量数据学习得来的。有些数据并不是从现实世界中收集而来，而是由计算机程序自己生成，例如，在AlphaGo算法训练的过程中，它和自己对弈了数百万局，这个数量大大超过了所有记录下来的职业选手棋谱的数量。

1.2.2 范式各阶段的应用⚓︎

作为一个小例子，我们可以看看各个阶段的方法论如何解一个我们姑且称为“智能之门” $^{[6]}$ 的问题：

顾客参加一个抽奖活动，三个关闭的门后面只有一个有奖品，顾客选择一个门之后，主持人会打开一个没有奖品的门，并给顾客一次改变选择的机会。此时，改选另外一个门会得到更大的获奖几率么？如图1-10所示。

图1-10 智能之门

怎么解决这个问题呢？我们用各种范式来看看：

经验归纳⚓︎

我们生活中的确碰到过各种抽奖时刻，有时候我们看似有很多赚大钱的机会，但是往往赢家不是自己。从这些生活经验出发，我们的直觉告诉我们要怎么选择呢？（我们做了调查，同学们的“基于生活经验的直觉”是这样分布的：X：Y）很多人会是从生活经验出发，感觉自己会中计，因此决定“我换了就上当了，我不换”，“我改变选择对运气不好，我不换”。当然，我们还可以用类比推理的办法，如果是100扇门，只有一扇门后面有奖品，我选中了一扇门，裁判打开了另外98个没有奖品的门，这个时候，我要换门么？

理论推导⚓︎

本书的读者大多学过基本的概率知识，我们可以用概率的基本方法来解这一道题目。

设 $A$ 为第一次选到了中奖门的概率， $B$ 为改变选择后选到了中奖门的概率， $C$ 为未改变选择后选到了中奖门的概率。

$\displaystyle P(A)=\frac{1}{3}$ （初始选择就是获奖门的获奖概率是 $\displaystyle \frac{1}{3}$ ）

$\displaystyle P(A')=\frac{2}{3}$ （当选中一个门之后，其它两个门的获奖概率是 $\displaystyle \frac{2}{3}$ ）

$P(B|A)=0$ （用户先选择了一个门，奖品在这个门后，用户后来改变选择，他的获奖概率是 $0$ ）

$P(C|A)=1$ （用户选择了一个门，奖品在门后，后来他不改变选择，他的获奖概率是 $1$ ）

$P(B|A')=1$ ， $P(C|A')=0$ （类似地，用户首次选择的门后面没有奖品，他改变选择后，获奖概率是 $1$ ，不改变选择，那么获奖概率是 $0$ ）

$\displaystyle P(B)=P(B|A) \times P(A) + P(B|A') \times P(A')=\frac{2}{3}$ （所以，改变选择后中奖的概率，等于 $\displaystyle \frac{2}{3}$ ）

$\displaystyle P(C)=P(C|A') \times P(A') + P(C|A) \times P(A)=\frac{1}{3}$ （不改变选择而中奖的概率，等于 $\displaystyle \frac{1}{3}$ ，和 $A$ 一样）

结论： $P(B)>P(C)$

数据模拟⚓︎

我们还可以用数据模拟的方法，来看看在各种情况下，换或者不换的结果如何。

看我们的Python程序示例，如图1-11所示。

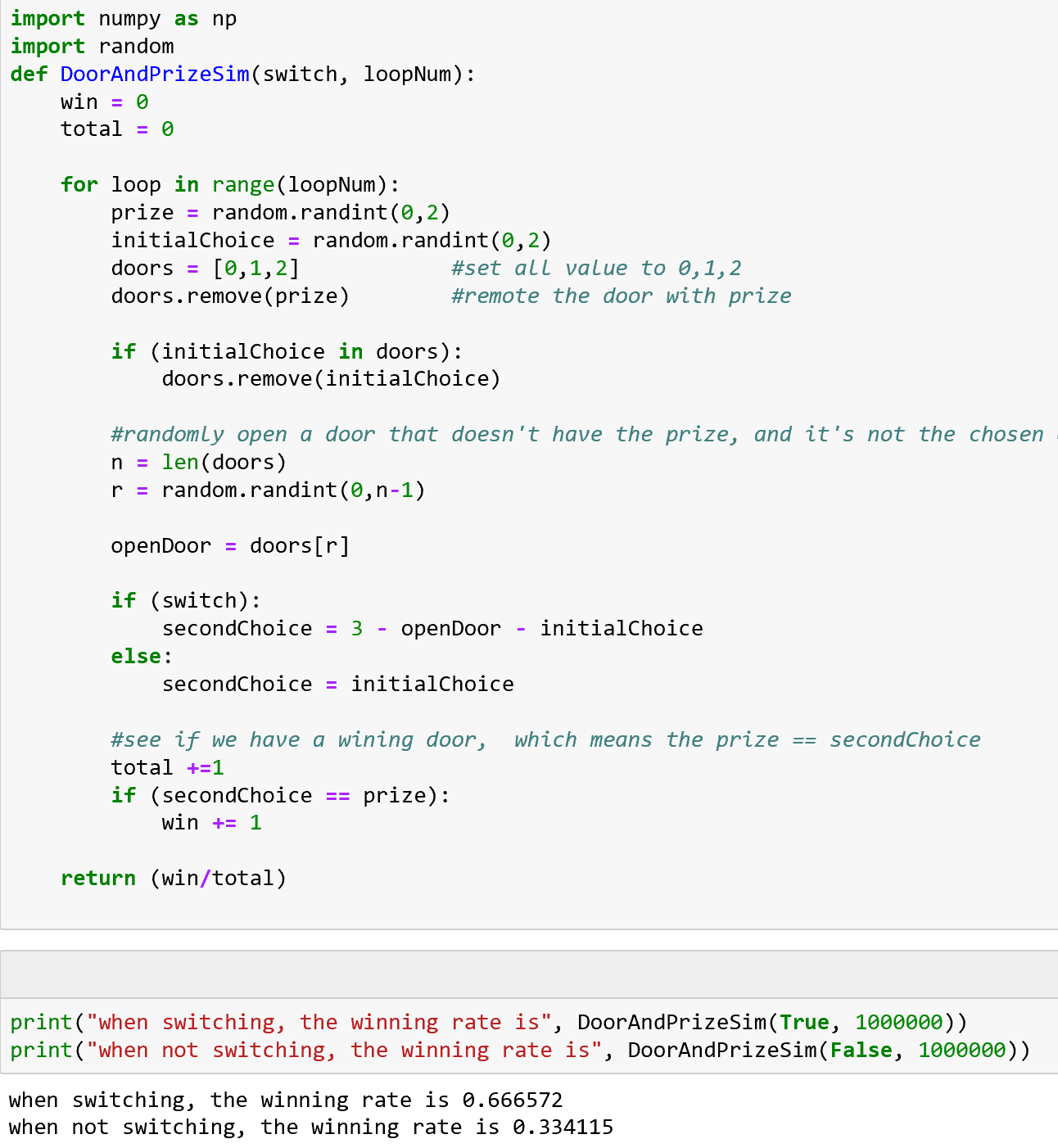
图1-11 用程序模拟智能之门问题

我们看到，当我们随机模拟一百万轮换门（switching）和不换门（not switching）的情况后，我们得到了这样的结果：

换门：最后得奖的概率是 $0.666572$ （约 $\displaystyle \frac{2}{3}$ ）
不换门：最后得奖的概率是 $0.334115$ （约 $\displaystyle \frac{1}{3}$ ）

数据探索⚓︎

当人类探索客观世界的时候，大部分情况下，我们是不了解新环境的运行规则的。这个时候，我们可以观察自己的行动和客观世界的反馈，判断得失，再总结出规律。这种学习方法，叫强化学习（Reinforcement Learning），可以使用这种方法来找出适合的策略。

我们假设顾客就是图1-12的行动者（Agent），他身处环境中，有一定的状态，他为了达到一定的目的（总的奖励），不断地采取一系列的动作去尝试与环境进行交互，这些交互会给他带来奖励，同时改变他的状态，他可以交互中根据反馈不断地调整策略，试图了解到状态、动作和总的奖励关系。强化学习可以通过表格来跟踪和调整这些关系（例如Q-Learning方法）或者通过神经网络来达到同样的目的。

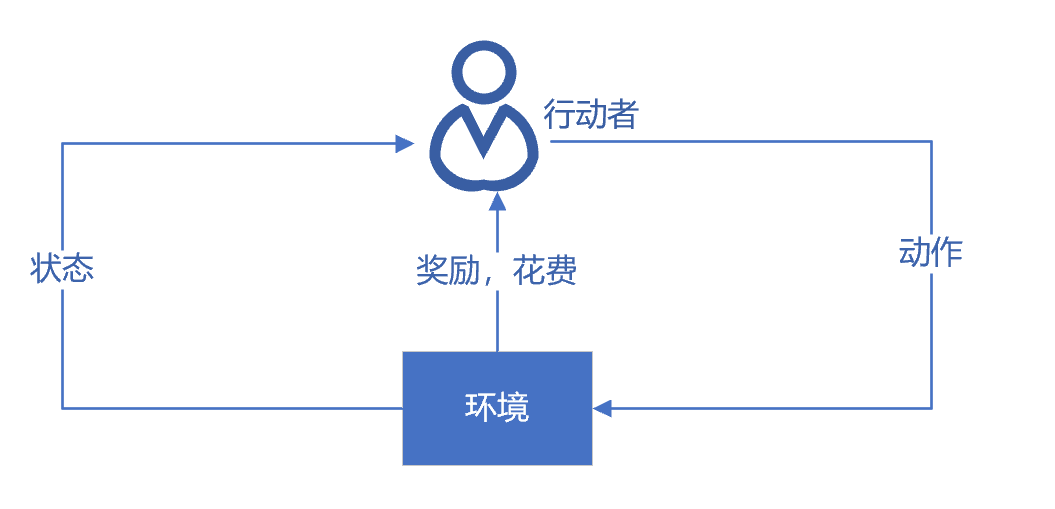
图1-12 强化学习示意图

下面是伪代码的程序示例（使用Q-Learning的方法）：

//维护一个表格，命名为Q，存储Agent所在的“状态”和“收益”
1. 起始状态，表格Q所有内容都清零 
2. 在每一个选择的机会时候 
3.   查找目前状态中可能收益最大的动作
4.   执行动作，得到收益，进入下一个状态
5.   按照规则，更新表格Q 中的收益，规则是
6.     新收益 = 原来的收益 + （新收益 +未来可能获得的最大收益）* 折扣率

完整的可执行代码在网上社区里找到。通过学习和运行示例程序，我们看到这段程序通过强化学习的手段和客观环境交互，学到了一个获利机会更大的策略。这个过程，和大家玩游戏是不是很类似呢？

从这个例子和我们最初看到的依赖事先设计好的逻辑的聊天程序，和依赖事先准备好的数据的“中文房间”程序，很不一样，这个例子中程序是从和环境交互的过程中学习，不断完善。当然，深度学习还有很多更强有力的学习方法，我们在下面的章节中，我们一步一步地介绍。如何构建各种神经网络，完成各种层次的数据探索任务。