07.4 线性多分类结果可视化
7.4 多分类结果可视化⚓︎
神经网络到底是一对一方式,还是一对多方式呢?从Softmax公式,好像是一对多方式,因为只取一个最大值,那么理想中的一对多方式应该是图7-13所示的样子。
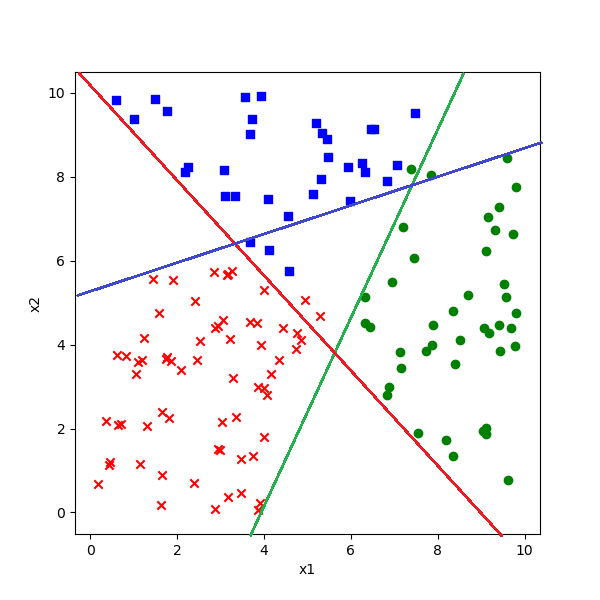
图7-13 理想中的一对多方式的分割线
实际上是什么样子的,我们来看下面的具体分析。
7.4.1 显示原始数据图⚓︎
与二分类时同样的问题,如何直观地理解多分类的结果?三分类要复杂一些,我们先把原始数据显示出来。
def ShowData(X,Y):
for i in range(X.shape[0]):
if Y[i,0] == 1:
plt.plot(X[i,0], X[i,1], '.', c='r')
elif Y[i,0] == 2:
plt.plot(X[i,0], X[i,1], 'x', c='g')
elif Y[i,0] == 3:
plt.plot(X[i,0], X[i,1], '^', c='b')
# end if
# end for
plt.show()
会画出图7-1来。
7.4.2 显示分类结果分割线图⚓︎
下面的数据是神经网络训练出的权重和偏移值的结果:
......
epoch=98
98 1385 0.25640040547970516
epoch=99
99 1399 0.2549651316913006
W= [[-1.43299777 -3.57488388 5.00788165]
[ 4.47527075 -2.88799216 -1.58727859]]
B= [[-1.821679 3.66752583 -1.84584683]]
......
其实在7.2节中讲解多分类原理的时候,我们已经解释了其几何理解,那些公式的推导就可以用于指导我们画出多分类的分割线来。先把几个有用的结论拿过来。
从7.2节中的公式16,把不等号变成等号,即z_1=z_2,则代表了那条绿色的分割线,用于分割第一类和第二类的:
由于Python数组是从0开始的,所以公式1中的所有下标都减去1,写成代码:
b12 = (net.B[0,1] - net.B[0,0])/(net.W[1,0] - net.W[1,1])
w12 = (net.W[0,1] - net.W[0,0])/(net.W[1,0] - net.W[1,1])
从7.2节中的公式17,把不等号变成等号,即z_1=z_3,则代表了那条红色的分割线,用于分割第一类和第三类的:
写成代码:
b13 = (net.B[0,0] - net.B[0,2])/(net.W[1,2] - net.W[1,0])
w13 = (net.W[0,0] - net.W[0,2])/(net.W[1,2] - net.W[1,0])
从7.2节中的公式24,把不等号变成等号,即z_2=z_3,则代表了那条蓝色的分割线,用于分割第二类和第三类的:
写成代码:
b23 = (net.B[0,2] - net.B[0,1])/(net.W[1,1] - net.W[1,2])
w23 = (net.W[0,2] - net.W[0,1])/(net.W[1,1] - net.W[1,2])
完整代码请看ch07 Level2的python文件。
改一下主函数,增加对以上两个函数ShowData()和ShowResult()的调用,最后可以看到图7-14所示的分类结果图,注意,这个结果图和我们在7.2中分析的一样,只是蓝线斜率不同。
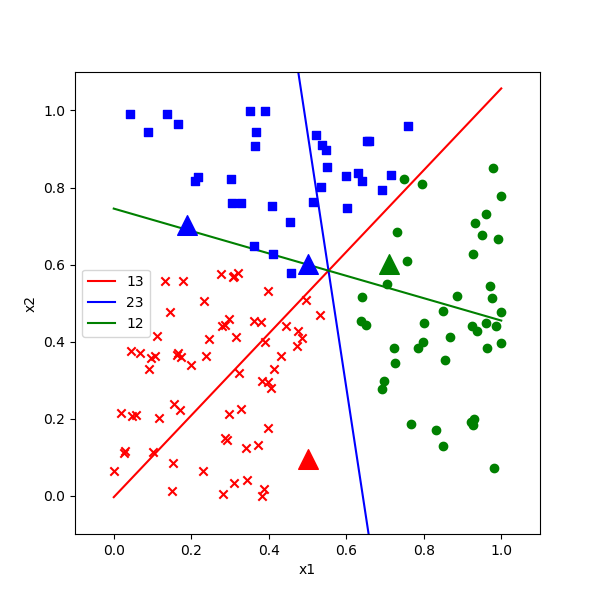
图7-14 神经网络绘出的分类结果图
图7-14中的四个三角形的大点是需要我们预测的四个坐标值,其中三个点的分类都比较明确,只有那个蓝色的点看不清在边界那一侧,可以通过在实际的运行结果图上放大局部来观察。
7.4.3 理解神经网络的分类方式⚓︎
做为实际结果,图7-14与我们猜想的图7-13完全不同:
- 蓝色线是2|3的边界,不考虑第1类
- 绿色线是1|2的边界,不考虑第3类
- 红色线是1|3的边界,不考虑第2类
我们只看蓝色的第1类,当要区分1|2和1|3时,神经网络实际是用了两条直线(绿色和红色)同时作为边界。那么它是一对一方式还是一对多方式呢?
图7-14的分割线是我们令z_1=z_2, z_2=z_3, z_3=z_1三个等式得到的,但实际上神经网络的工作方式不是这样的,它不会单独比较两类,而是会同时比较三类,这个从Softmax会同时输出三个概率值就可以理解。比如,当我们想得到第一类的分割线时,需要同时满足两个条件:
即,同时,找到第一类和第三类的边界。
这就意味着公式4其实是一个线性分段函数,而不是两条直线,即图7-15中红色射线和绿色射线所组成的函数。
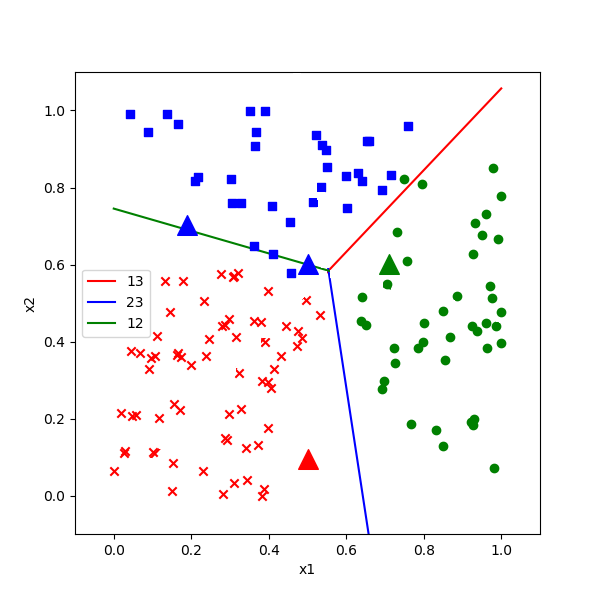
图7-15 分段线性的分割作用
同理,用于分开红色点和其它两类的分割线是蓝色射线和绿色射线,用于分开绿色点和其它两类的分割线是红色射线和蓝色射线。
训练一对多分类器时,是把蓝色样本当作一类,把红色和绿色样本混在一起当作另外一类。训练一对一分类器时,是把绿色样本扔掉,只考虑蓝色样本和红色样本。而我们在此并没有这样做,三类样本是同时参与训练的。所以我们只能说神经网络从结果上看,是一种一对多的方式,至于它的实质,我们在后面的非线性分类时再进一步探讨。
代码位置⚓︎
ch07, Level2
思考与练习⚓︎
- 使用一对一的方法训练三个二分类器,来解决此问题。