第5章 多入单出的单层神经网络 - 多变量线性回归⚓︎
5.0 多变量线性回归问题⚓︎
5.0.1 提出问题⚓︎
问题:在北京通州,距离通州区中心15公里的一套93平米的房子,大概是多少钱?
房价预测问题,成为了机器学习的一个入门话题,著名的波士顿的房价数据及相关的比赛已经很多了,但是美国的房子都是独栋的,前院后院停车库游泳池等等参数非常多,初学者可能理解起来有困难。我们不妨用简化版的北京通州的房价来举例,感受一下房价预测的过程。
影响北京通州房价的因素有很多,居住面积、地理位置、朝向、学区房、周边设施、建筑年份等等,其中,面积和地理位置是两个比较重要的因素。地理位置信息一般采用经纬度方式表示,但是经纬度是两个特征值,联合起来才有意义,因此,我们把它转换成了到通州区中心的距离。
我们有1000个样本,每个样本有两个特征值,一个标签值,示例如表5-1。
表5-1 样本数据
| 样本序号 | 地理位置 | 居住面积 | 价格(万元) |
|---|---|---|---|
| 1 | 10.06 | 60 | 302.86 |
| 2 | 15.47 | 74 | 393.04 |
| 3 | 18.66 | 46 | 270.67 |
| 4 | 5.20 | 77 | 450.59 |
| ... | ... | ... | ... |
- 特征值1 - 地理位置,统计得到:
- 最大值:21.96公里
- 最小值:2.02公里
-
平均值:12.13公里
-
特征值2 - 房屋面积,统计得到:
- 最大值:119平米
- 最小值:40平米
-
平均值:78.9平米
-
标签值 - 房价,单位为百万元:
- 最大值:674.37
- 最小值:181.38
- 平均值:420.64
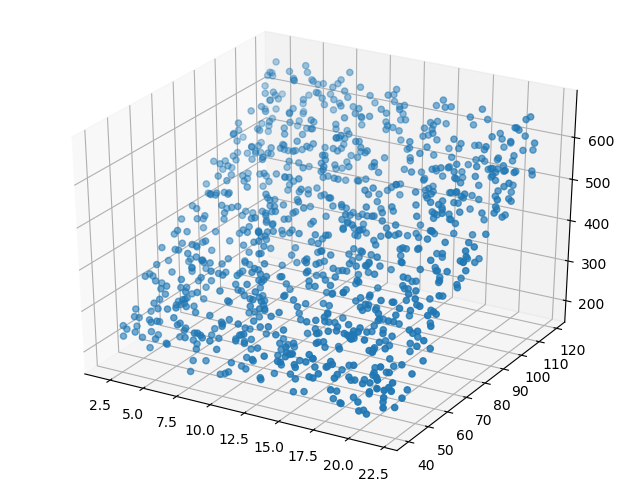
这个数据是三维的,所以可以用两个特征值作为 x 和 y,用标签值作为 z,在 xyz 坐标空间中展示如表5-2。
表5-2 样本在三维空间的可视化
| 正向 | 侧向 |
|---|---|
 |
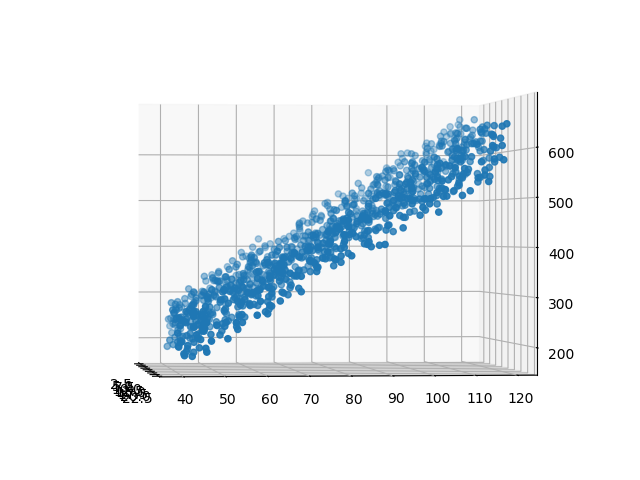 |
从正向看,很像一块草坪,似乎是一个平面。再从侧向看,和第4章中的直线拟合数据很像。所以,对于这种三维的线性拟合,我们可以把它想象成为拟合一个平面,这个平面会位于这块“草坪”的中位,把“草坪”分割成上下两块更薄的“草坪”,最终使得所有样本点到这个平面的距离的平方和最小。
5.0.2 多元线性回归模型⚓︎
由于表中可能没有恰好符合15公里、93平米条件的数据,因此我们需要根据1000个样本值来建立一个模型,来解决预测问题。
通过图示,我们基本可以确定这个问题是个线性回归问题,而且是典型的多元线性回归,即包括两个或两个以上自变量的回归。多元线性回归的函数模型如下:
具体化到房价预测问题,上面的公式可以简化成:
抛开本例的房价问题,对于一般的应用问题,建立多元线性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变量的选择,其准则是:
- 自变量对因变量必须有显著的影响,并呈密切的线性相关;
- 自变量与因变量之间的线性相关必须是真实的,而不是形式上的;
- 自变量之间应具有一定的互斥性,即自变量之间的相关程度不应高于自变量与因变量之因的相关程度;
- 自变量应具有完整的统计数据,其预测值容易确定。
5.0.3 解决方案⚓︎
如果用传统的数学方法解决这个问题,我们可以使用正规方程,从而可以得到数学解析解,然后再使用神经网络方式来求得近似解,从而比较两者的精度,再进一步调试神经网络的参数,达到学习的目的。
我们不妨先把两种方式在这里做一个对比,读者阅读并运行代码,得到结果后,再回到这里来仔细体会表5-3中的比较项。
表5-3 两种方法的比较
| 方法 | 正规方程 | 梯度下降 |
|---|---|---|
| 原理 | 几次矩阵运算 | 多次迭代 |
| 特殊要求 | X^{\top}X 的逆矩阵存在 | 需要确定学习率 |
| 复杂度 | O(n^3) | O(n^2) |
| 适用样本数 | m \lt 10000 | m \ge 10000 |