02.3 梯度下降
2.3 梯度下降⚓︎
2.3.1 从自然现象中理解梯度下降⚓︎
在大多数文章中,都以“一个人被困在山上,需要迅速下到谷底”来举例,这个人会“寻找当前所处位置最陡峭的地方向下走”。这个例子中忽略了安全因素,这个人不可能沿着最陡峭的方向走,要考虑坡度。
在自然界中,梯度下降的最好例子,就是泉水下山的过程:
- 水受重力影响,会在当前位置,沿着最陡峭的方向流动,有时会形成瀑布(梯度下降);
- 水流下山的路径不是唯一的,在同一个地点,有可能有多个位置具有同样的陡峭程度,而造成了分流(可以得到多个解);
- 遇到坑洼地区,有可能形成湖泊,而终止下山过程(不能得到全局最优解,而是局部最优解)。
2.3.2 梯度下降的数学理解⚓︎
梯度下降的数学公式:
\theta_{n+1} = \theta_{n} - \eta \cdot \nabla J(\theta) \tag{1}
其中:
- \theta_{n+1}:下一个值;
- \theta_n:当前值;
- -:减号,梯度的反向;
- \eta:学习率或步长,控制每一步走的距离,不要太快以免错过了最佳景点,不要太慢以免时间太长;
- \nabla:梯度,函数当前位置的最快上升点;
- J(\theta):函数。
梯度下降的三要素⚓︎
- 当前点;
- 方向;
- 步长。
为什么说是“梯度下降”?⚓︎
“梯度下降”包含了两层含义:
- 梯度:函数当前位置的最快上升点;
- 下降:与导数相反的方向,用数学语言描述就是那个减号。
亦即与上升相反的方向运动,就是下降。
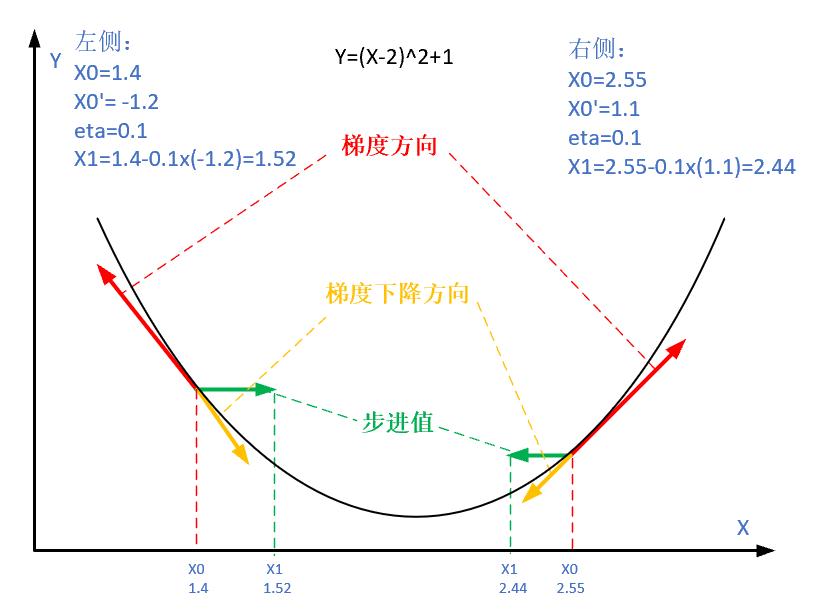
图2-9 梯度下降的步骤
图2-9解释了在函数极值点的两侧做梯度下降的计算过程,梯度下降的目的就是使得x值向极值点逼近。
2.3.3 单变量函数的梯度下降⚓︎
假设一个单变量函数:
J(x) = x ^2
我们的目的是找到该函数的最小值,于是计算其微分:
J'(x) = 2x
假设初始位置为:
x_0=1.2
假设学习率:
\eta = 0.3
根据公式(1),迭代公式:
x_{n+1} = x_{n} - \eta \cdot \nabla J(x)= x_{n} - \eta \cdot 2x
假设终止条件为 J(x)<0.01,迭代过程是:
x=0.480000, y=0.230400
x=0.192000, y=0.036864
x=0.076800, y=0.005898
x=0.030720, y=0.000944
上面的过程如图2-10所示。
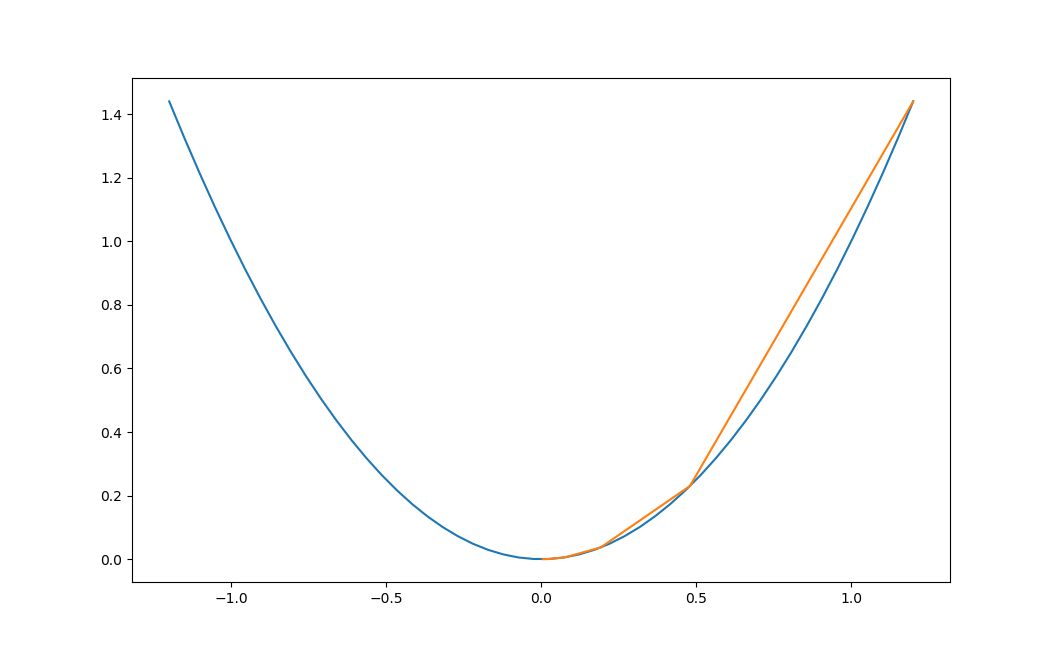
图2-10 使用梯度下降法迭代的过程
2.3.4 双变量的梯度下降⚓︎
假设一个双变量函数:
J(x,y) = x^2 + \sin^2(y)
我们的目的是找到该函数的最小值,于是计算其微分:
{\partial{J(x,y)} \over \partial{x}} = 2x$$
$${\partial{J(x,y)} \over \partial{y}} = 2 \sin y \cos y
假设初始位置为:
(x_0,y_0)=(3,1)
假设学习率:
\eta = 0.1
根据公式(1),迭代过程是的计算公式:
(x_{n+1},y_{n+1}) = (x_n,y_n) - \eta \cdot \nabla J(x,y)
= (x_n,y_n) - \eta \cdot (2x,2 \cdot \sin y \cdot \cos y) \tag{1}
根据公式(1),假设终止条件为 J(x,y)<0.01,迭代过程如表2-3所示。
表2-3 双变量梯度下降的迭代过程
| 迭代次数 | x | y | J(x,y) |
|---|---|---|---|
| 1 | 3 | 1 | 9.708073 |
| 2 | 2.4 | 0.909070 | 6.382415 |
| ... | ... | ... | ... |
| 15 | 0.105553 | 0.063481 | 0.015166 |
| 16 | 0.084442 | 0.050819 | 0.009711 |
迭代16次后,J(x,y) 的值为 0.009711,满足小于 0.01 的条件,停止迭代。
上面的过程如表2-4所示,由于是双变量,所以需要用三维图来解释。请注意看两张图中间那条隐隐的黑色线,表示梯度下降的过程,从红色的高地一直沿着坡度向下走,直到蓝色的洼地。
表2-4 在三维空间内的梯度下降过程
| 观察角度1 | 观察角度2 |
|---|---|
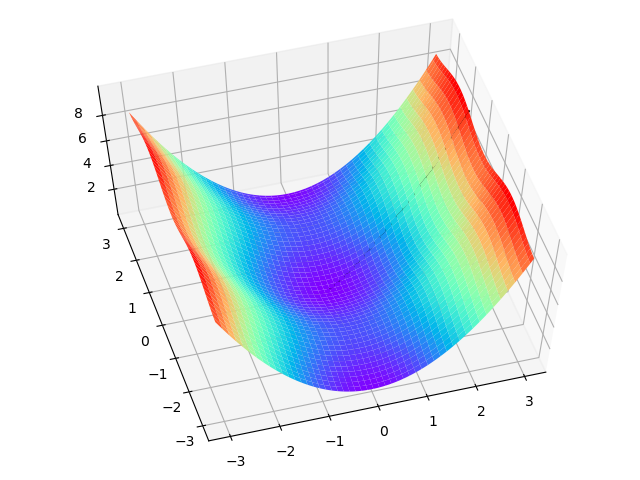 |
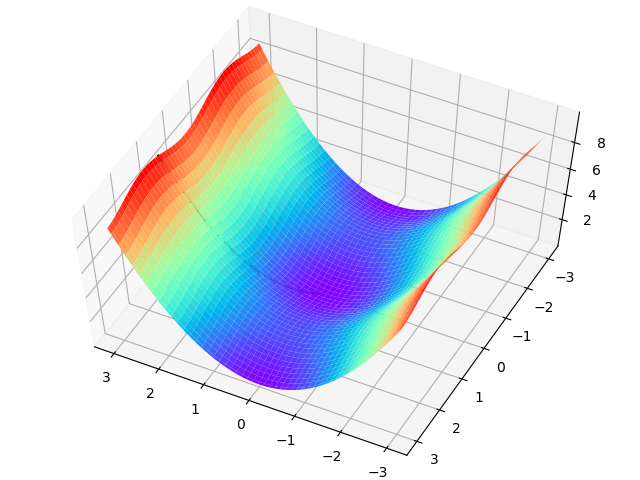 |
2.3.5 学习率η的选择⚓︎
在公式表达时,学习率被表示为\eta。在代码里,我们把学习率定义为learning_rate,或者eta。针对上面的例子,试验不同的学习率对迭代情况的影响,如表2-5所示。
表2-5 不同学习率对迭代情况的影响
| 学习率 | 迭代路线图 | 说明 |
|---|---|---|
| 1.0 | 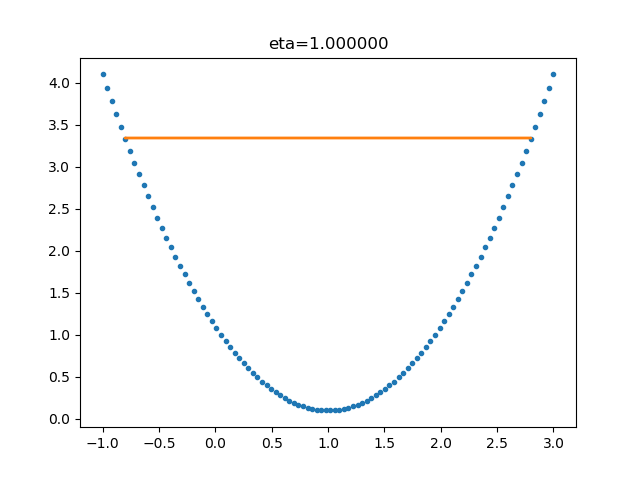 |
学习率太大,迭代的情况很糟糕,在一条水平线上跳来跳去,永远也不能下降。 |
| 0.8 | 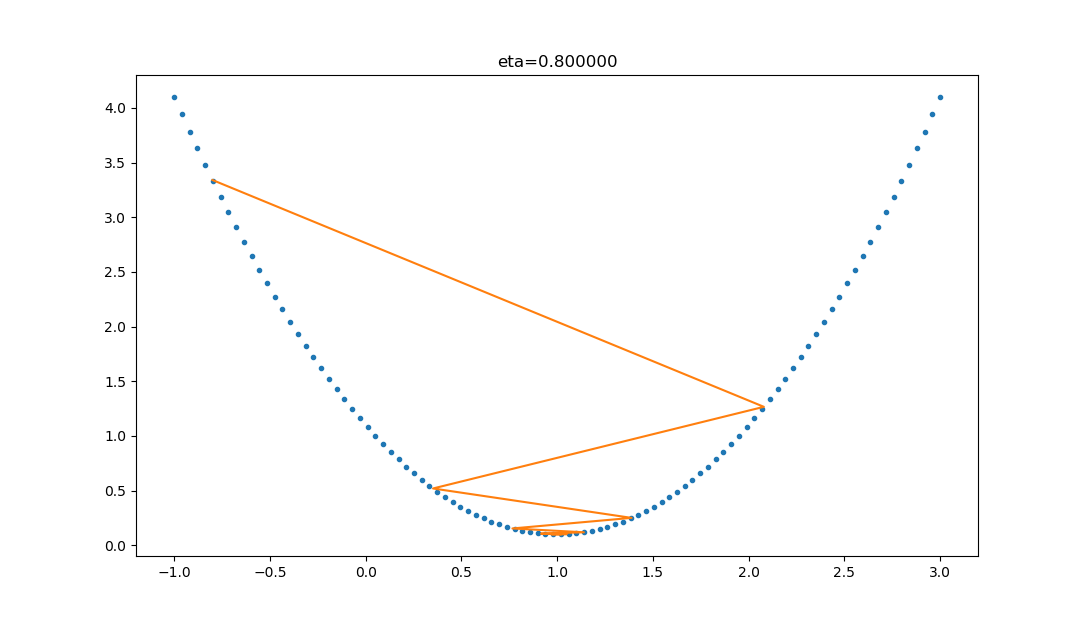 |
学习率大,会有这种左右跳跃的情况发生,这不利于神经网络的训练。 |
| 0.4 | 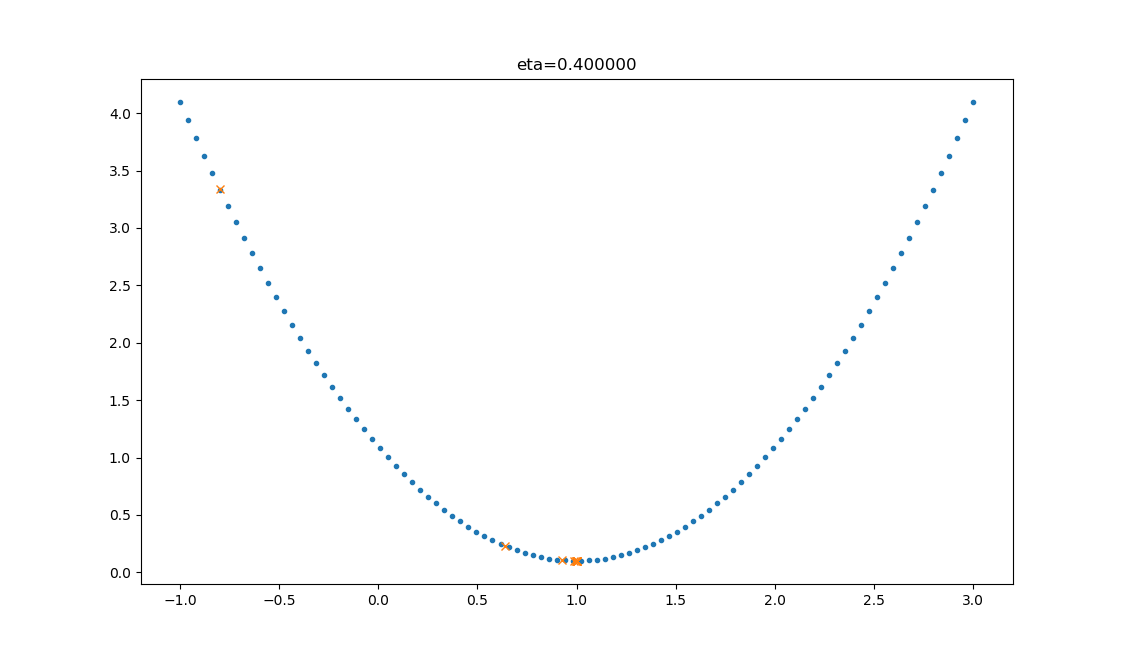 |
学习率合适,损失值会从单侧下降,4步以后基本接近了理想值。 |
| 0.1 | 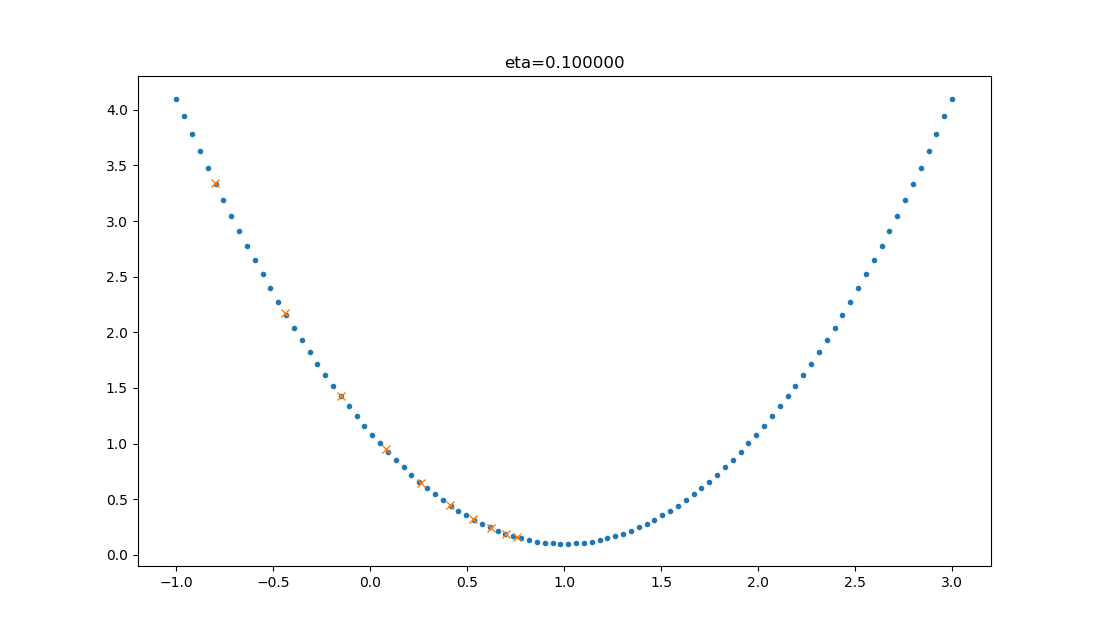 |
学习率较小,损失值会从单侧下降,但下降速度非常慢,10步了还没有到达理想状态。 |
代码位置⚓︎
ch02, Level3, Level4, Level5