第16章 正则化⚓︎
正则化的英文为Regularization,用于防止过拟合。
16.0 过拟合⚓︎
16.0.1 拟合程度比较⚓︎
在深度神经网络中,我们遇到的另外一个挑战,就是网络的泛化问题。所谓泛化,就是模型在测试集上的表现要和训练集上一样好。经常有这样的例子:一个模型在训练集上千锤百炼,能到达99%的准确率,拿到测试集上一试,准确率还不到90%。这说明模型过度拟合了训练数据,而不能反映真实世界的情况。解决过度拟合的手段和过程,就叫做泛化。
神经网络的两大功能:回归和分类。这两类任务,都会出现欠拟合和过拟合现象,如图16-1和16-2所示。
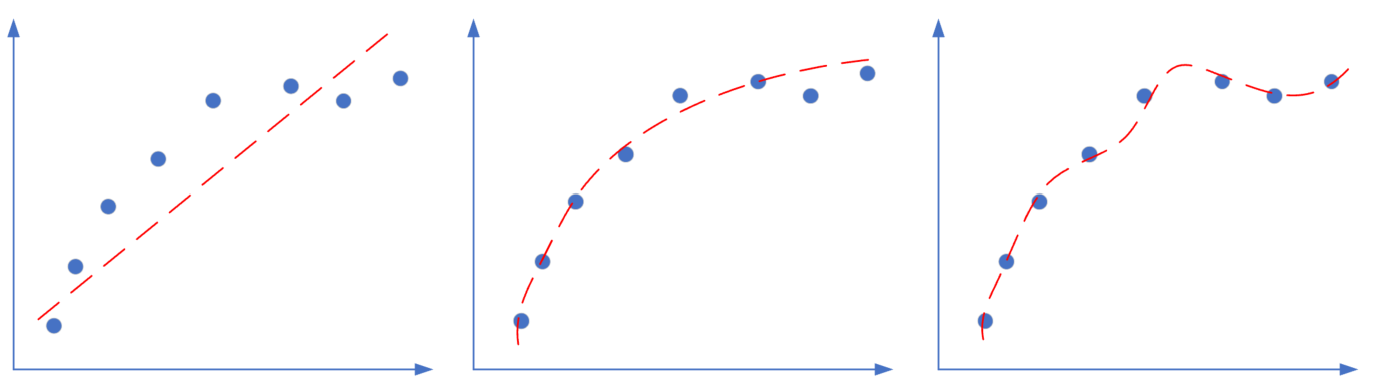
图16-1 回归任务中的欠拟合、正确的拟合、过拟合
图16-1是回归任务中的三种情况,依次为:欠拟合、正确的拟合、过拟合。
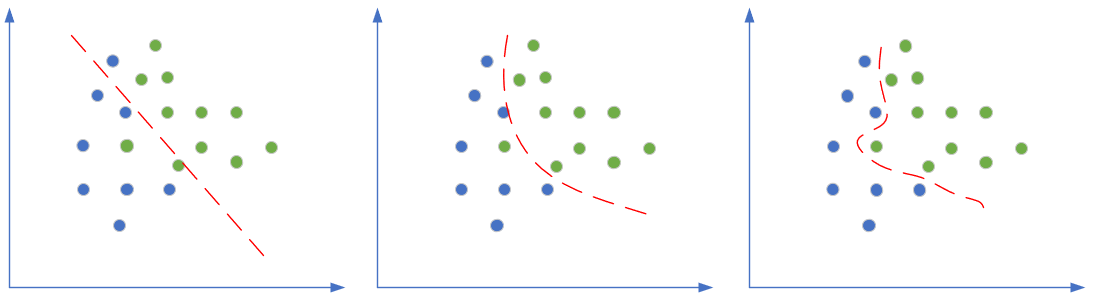
图16-2 分类任务中的欠拟合、正确的拟合、过拟合
图16-2是分类任务中的三种情况,依次为:分类欠妥、正确的分类、分类过度。由于分类可以看作是对分类边界的拟合,所以我们经常也统称其为拟合。
上图中对于“深入敌后”的那颗绿色点样本,正确的做法是把它当作噪音看待,而不要让它对网络产生影响。而对于上例中的欠拟合情况,如果简单的(线性)模型不能很好地完成任务,我们可以考虑使用复杂的(非线性或深度)模型,即加深网络的宽度和深度,提高神经网络的能力。
但是如果网络过于宽和深,就会出现第三张图展示的过拟合的情况。
出现过拟合的原因:
- 训练集的数量和模型的复杂度不匹配,样本数量级小于模型的参数
- 训练集和测试集的特征分布不一致
- 样本噪音大,使得神经网络学习到了噪音,正常样本的行为被抑制
- 迭代次数过多,过分拟合了训练数据,包括噪音部分和一些非重要特征
既然模型过于复杂,那么我们简化模型不就行了吗?为什么要用复杂度不匹配的模型呢?有两个原因:
- 因为有的模型以及非常成熟了,比如VGG16,可以不调参而直接用于你自己的数据训练,此时如果你的数据数量不够多,但是又想使用现有模型,就需要给模型加正则项了。
- 使用相对复杂的模型,可以比较快速地使得网络训练收敛,以节省时间。
16.0.2 过拟合的例子一⚓︎
充分理解过拟合的原因之后,我们先制作一个数据集,让其符合上面的第三条:制造样本噪音。但是如何制作一个合理的噪音呢?这让笔者想起了一篇讲解傅里叶变换的文章,一个复合的傅里叶变换公式可以是这样的:
这个公式可以在[0,2\pi]之间制作出图16-3。
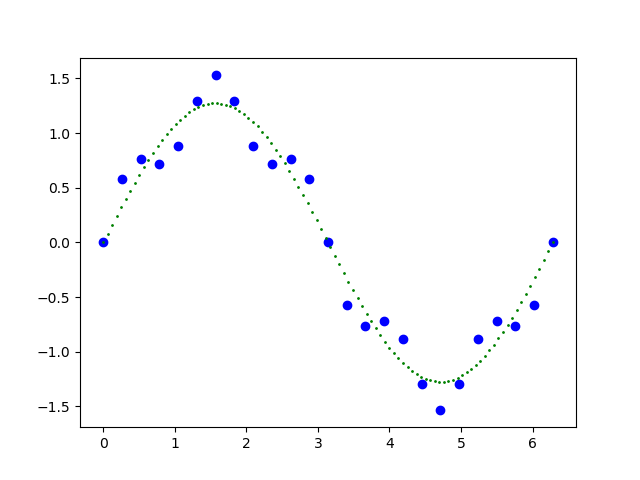
图16-3 公式1的函数图
其中,绿色的点是公式1的第一部分的结果,蓝色的点是整个公式1的结果。我们可以把绿色的点作为测试/验证基线,可以看到它是一条标准的正弦曲线。而蓝色的点作为带噪音的训练样本,该训练样本只有25个数据。
然后我们使用MiniFramework,可以很方便地搭建起下面这个模型,如图16-4。
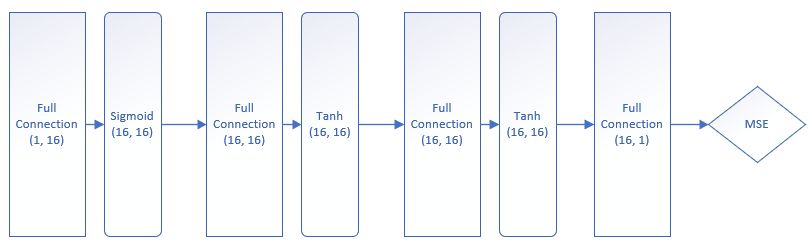
图16-4 用于拟合公式1的模型结构
这个模型的复杂度要比训练样本级大很多,所以可以重现过拟合的现象,当然还需要设置好合适的参数,代码片段如下:
def SetParameters():
num_hidden = 16
max_epoch = 20000
batch_size = 5
learning_rate = 0.1
eps = 1e-6
hp = HyperParameters41(
learning_rate, max_epoch, batch_size, eps,
net_type=NetType.Fitting,
init_method=InitialMethod.Xavier,
optimizer_name=OptimizerName.SGD)
return hp, num_hidden
我们故意把最大epoch次数设置得比较大,以充分展示过拟合效果。训练结束后,首先看损失函数值和精度值的变化曲线,如图16-5所示。
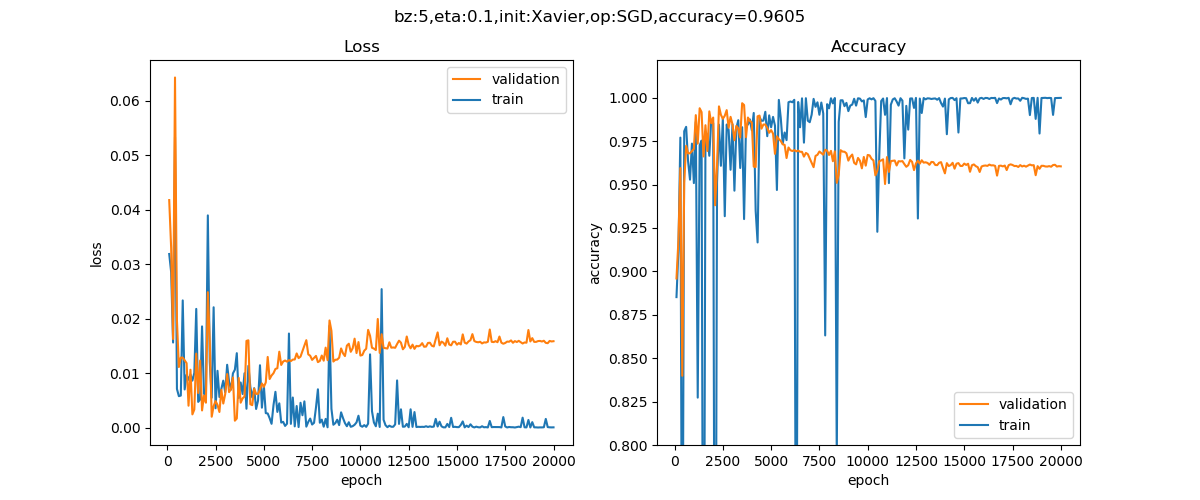
图16-5 损失函数值和精度值的变化曲线
蓝色为训练集,红色为验证集。可以看到,训练集上的损失函数值很快降低到极点,精确度很快升高到极点,而验证集上的表现正好相反。说明网络对训练集很适应,但是越来越不适应验证集数据,出现了严重的过拟合。验证集的精确度为0.9605。
再看下图的拟合情况,如图16-6所示。
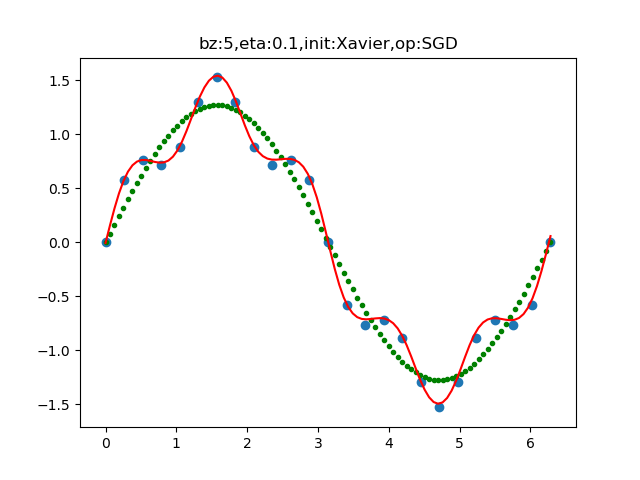
图16-6 模型的拟合情况
红色拟合曲线严丝合缝地拟合了每一个样本点,也就是说模型学习到了样本的误差。绿色点所组成的曲线,才是我们真正想要的拟合结果。
16.0.3 过拟合的例子二⚓︎
运行本例子前需要把前面的关于 MNIST 的 4 个数据文件拷贝到 "ch16-DnnRegularization\ExtendedDataReader\data\" 目录下。
我们将要使用MNIST数据集做例子,模拟出令一个过拟合(分类)的情况。从上面的过拟合出现的4点原因分析,第2点和第3点对于MNIST数据集来说并不成立,MNIST数据集有60000个样本,这足以保证它的特征分布的一致性,少数样本的噪音也会被大多数正常的数据所淹没。但是如果我们只选用其中的很少一部分的样本,则特征分布就可能会有偏差,而且独立样本的噪音会变得突出一些。
再看过拟合原因中的第1点和第4点,我们利用第14章中的已有知识和代码,搭建一个复杂网络很容易,而且迭代次数完全可以由代码来控制。
首先,只使用1000个样本来做训练,如下面的代码所示,调用一个ReadLessData(1000)函数,并且用GenerateValidationSet(k=10)函数把1000个样本分成900和100两部分,分别做为训练集和验证集:
def LoadData():
mdr = MnistImageDataReader(train_image_file, train_label_file, test_image_file, test_label_file, "vector")
mdr.ReadLessData(1000)
mdr.Normalize()
mdr.GenerateDevSet(k=10)
return mdr
然后,我们搭建一个深度网络,如图16-7所示。
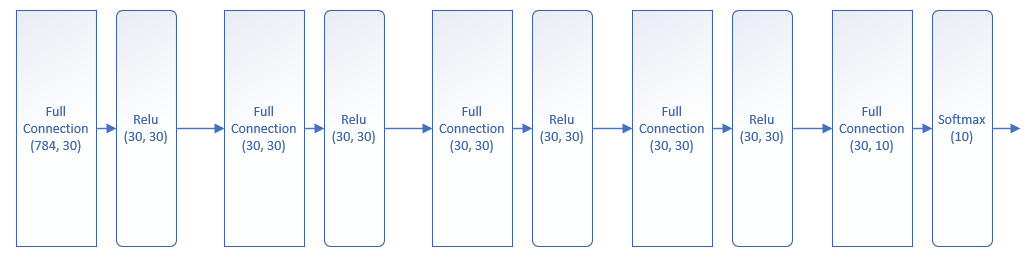
图16-7 过拟合例子二的深度网络模型结构
这个网络有5个全连接层,前4个全连接层后接ReLU激活函数层,最后一个全连接层接Softmax分类函数做10分类。由于我们在第14章就已经搭建好了深度神经网络的Mini框架,所以可以简单地搭建这个网络,如下代码所示:
def Net(dateReader, num_input, num_hidden, num_output, params):
net = NeuralNet(params)
fc1 = FcLayer(num_input, num_hidden, params)
net.add_layer(fc1, "fc1")
relu1 = ActivatorLayer(Relu())
net.add_layer(relu1, "relu1")
fc2 = FcLayer(num_hidden, num_hidden, params)
net.add_layer(fc2, "fc2")
relu2 = ActivatorLayer(Relu())
net.add_layer(relu2, "relu2")
fc3 = FcLayer(num_hidden, num_hidden, params)
net.add_layer(fc3, "fc3")
relu3 = ActivatorLayer(Relu())
net.add_layer(relu3, "relu3")
fc4 = FcLayer(num_hidden, num_hidden, params)
net.add_layer(fc4, "fc4")
relu4 = ActivatorLayer(Relu())
net.add_layer(relu4, "relu4")
fc5 = FcLayer(num_hidden, num_output, params)
net.add_layer(fc5, "fc5")
softmax = ActivatorLayer(Softmax())
net.add_layer(softmax, "softmax")
net.train(dataReader, checkpoint=1)
net.ShowLossHistory()
net.train(dataReader, checkpoint=1)函数的参数checkpoint的含义是,每隔1个epoch记录一次训练过程中的损失值和准确率。可以设置成大于1的数字,比如10,意味着每10个epoch检查一次。也可以设置为小于1大于0的数比如0.5,假设在一个epoch中要迭代100次,则每50次检查一次。
在main过程中,设置一些超参数,然后调用刚才建立的Net进行训练:
if __name__ == '__main__':
dataReader = LoadData()
num_feature = dataReader.num_feature
num_example = dataReader.num_example
num_input = num_feature
num_hidden = 30
num_output = 10
max_epoch = 200
batch_size = 100
learning_rate = 0.1
eps = 1e-5
params = CParameters(
learning_rate, max_epoch, batch_size, eps,
LossFunctionName.CrossEntropy3,
InitialMethod.Xavier,
OptimizerName.SGD)
Net(dataReader, num_input, num_hidden, num_hidden, num_hidden, num_hidden, num_output, params)
在超参数中,我们指定了:
- 每个隐层30个神经元(4个隐层在Net函数里指定)
- 最多训练200个
epoch - 批大小为100个样本
- 学习率为0.1
- 多分类交叉熵损失函数(CrossEntropy3)
- Xavier权重初始化方法
- 随机梯度下降算法
最终我们可以得到如图16-8所示的训练曲线。
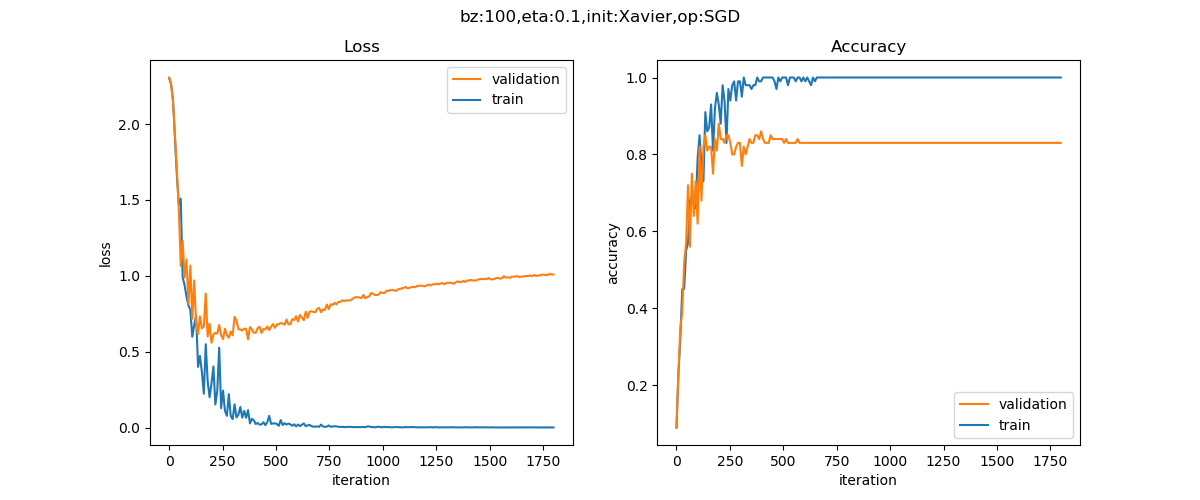
图16-8 过拟合例子二的训练曲线
在训练集上(蓝色曲线),很快就达到了损失函数值趋近于0,准确度100%的程度。而在验证集上(红色曲线),损失函数值却越来越大,准确度也在下降。这就造成了一个典型的过拟合网络,即所谓U型曲线,无论是损失函数值和准确度,都呈现出了这种分化的特征。
我们再看打印输出部分:
epoch=199, total_iteration=1799
loss_train=0.0015, accuracy_train=1.000000
loss_valid=0.9956, accuracy_valid=0.860000
time used: 5.082462787628174
total weights abs sum= 1722.470655813152
total weights = 26520
little weights = 2815
zero weights = 27
testing...
rate=8423 / 10000 = 0.8423
结果说明:
- 第199个
epoch上(从0开始计数,所以实际是第200个epoch),训练集的损失为0.0015,准确率为100%。测试集损失值0.9956,准确率86%。过拟合线性很严重。 total weights abs sum = 1722.4706,实际上是把所有全连接层的权重值先取绝对值,再求和。这个值和下面三个值在后面会有比较说明。total weights = 26520,一共26520个权重值,偏移值不算在内。little weights = 2815,一共2815个权重值小于0.01。zero weights = 27,是权重值中接近于0的数量(小于0.0001)。- 测试准确率为84.23%
在着手解决过拟合的问题之前,我们先来学习一下关于偏差与方差的知识,以便得到一些理论上的指导,虽然神经网络是一门实验学科。
16.0.4 解决过拟合问题⚓︎
有了直观感受和理论知识,下面我们看看如何解决过拟合问题:
- 数据扩展
- 正则
- 丢弃法
- 早停法
- 集成学习法
- 特征工程(属于传统机器学习范畴,不在此处讨论)
- 简化模型,减小网络的宽度和深度
代码位置⚓︎
ch16, Level0,Level1
思考与练习⚓︎
- 请采用简化模型的方式来试验上述两个过拟合案例。
参考资料⚓︎
- 周志华老师的西瓜书《机器学习》
- http://scott.fortmann-roe.com/docs/BiasVariance.html