第8章 激活函数⚓︎
8.0 激活函数概论⚓︎
在这一章,我们将简要介绍一下激活函数,因为在下一章中将要使用激活函数构造两层的神经网络。
8.0.1 激活函数的基本作用⚓︎
图8-1是神经网络中的一个神经元,假设该神经元有三个输入,分别为x_1,x_2,x_3,那么:
z=x_1 w_1 + x_2 w_2 + x_3 w_3 +b \tag{1}$$
$$a = \sigma(z) \tag{2}
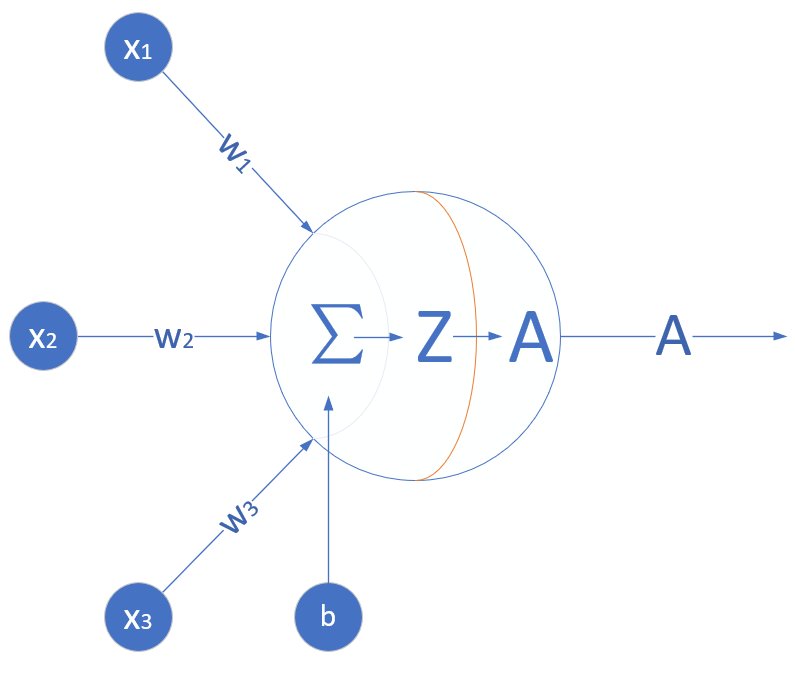
图8-1 激活函数在神经元中的位置
激活函数也就是 a=\sigma(z) 这一步了,他有什么作用呢?
- 给神经网络增加非线性因素,这个问题在第1章神经网络基本工作原理中已经讲过了;
- 把公式1的计算结果压缩到 [0,1] 之间,便于后面的计算。
激活函数的基本性质:
- 非线性:线性的激活函数和没有激活函数一样;
- 可导性:做误差反向传播和梯度下降,必须要保证激活函数的可导性;
- 单调性:单一的输入会得到单一的输出,较大值的输入得到较大值的输出。
在物理试验中使用的继电器,是最初的激活函数的原型:当输入电流大于一个阈值时,会产生足够的磁场,从而打开下一级电源通道,如图8-2所示。
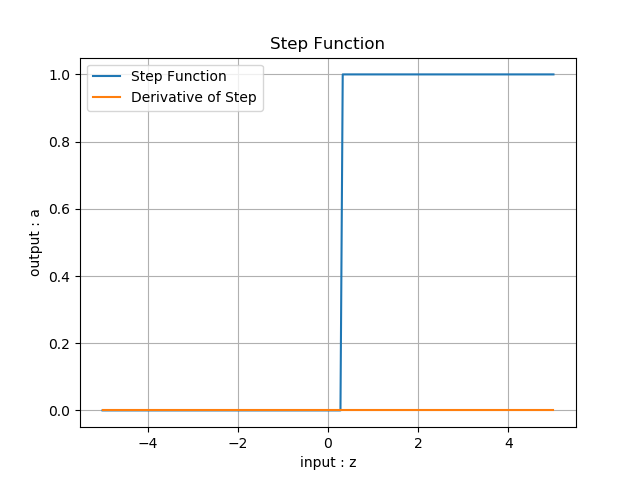
图8-2 继电器的阶跃形态
用到神经网络中的概念,用‘1’来代表一个神经元被激活,‘0’代表一个神经元未被激活。
这个Step函数有什么不好的地方呢?主要的一点就是,他的梯度(导数)恒为零(个别点除外)。反向传播公式中,梯度传递用到了链式法则,如果在这样一个连乘的式子其中有一项是零,这样的梯度就会恒为零,是没有办法进行反向传播的。
8.0.2 何时会用到激活函数⚓︎
激活函数用在神经网络的层与层之间的连接,神经网络的最后一层不用激活函数。
神经网络不管有多少层,最后的输出层决定了这个神经网络能干什么。在单层神经网络中,我们学习到了表8-1所示的内容。
表8-1 单层的神经网络的参数与功能
| 网络 | 输入 | 输出 | 激活函数 | 分类函数 | 功能 |
|---|---|---|---|---|---|
| 单层 | 单变量 | 单输出 | 无 | 无 | 线性回归 |
| 单层 | 多变量 | 单输出 | 无 | 无 | 线性回归 |
| 单层 | 多变量 | 单输出 | 无 | 二分类函数 | 二分类 |
| 单层 | 多变量 | 多输出 | 无 | 多分类函数 | 多分类 |
从上表可以看到,我们一直没有使用激活函数,而只使用了分类函数。对于多层神经网络也是如此,在最后一层只会用到分类函数来完成二分类或多分类任务,如果是拟合任务,则不需要分类函数。
简言之:
- 神经网络最后一层不需要激活函数
- 激活函数只用于连接相邻的两层神经网络
在后面的章节中,当不需要指定具体的激活函数形式时,会使用 \sigma() 符号来代表激活函数运算。