07.2 线性多分类实现
7.2 线性多分类的神经网络实现⚓︎
7.2.1 定义神经网络结构⚓︎
从图7-1来看,似乎在三个颜色区间之间有两个比较明显的分界线,而且是直线,即线性可分的。我们如何通过神经网络精确地找到这两条分界线呢?
- 从视觉上判断是线性可分的,所以我们使用单层神经网络即可
- 输入特征有两个,分别为经度、纬度
- 最后输出的是三个分类,分别是魏蜀吴,所以输出层有三个神经元
如果有三个以上的分类同时存在,我们需要对每一类别分配一个神经元,这个神经元的作用是根据前端输入的各种数据,先做线性处理(Z=WX+B),然后做一次非线性处理,计算每个样本在每个类别中的预测概率,再和标签中的类别比较,看看预测是否准确,如果准确,则奖励这个预测,给与正反馈;如果不准确,则惩罚这个预测,给与负反馈。两类反馈都反向传播到神经网络系统中去调整参数。
这个网络只有输入层和输出层,由于输入层不算在内,所以是一层网络,如图7-7所示。
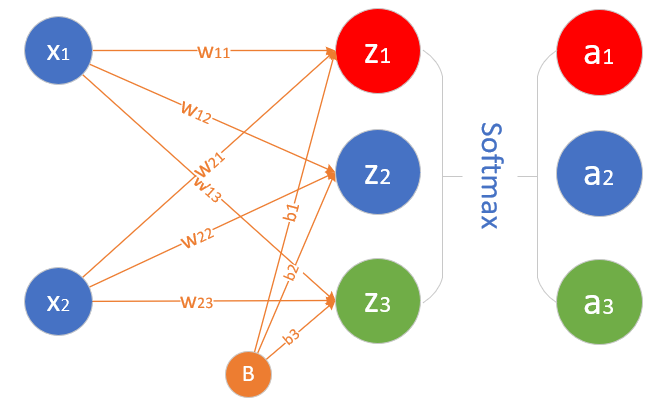
图7-7 多入多出单层神经网络
与前面的单层网络不同的是,图7-7最右侧的输出层还多出来一个Softmax分类函数,这是多分类任务中的标准配置,可以看作是输出层的激活函数,并不单独成为一层,与二分类中的Logistic函数一样。
输入层⚓︎
输入经度 x_1 和纬度 x_2 两个特征:
权重矩阵⚓︎
W权重矩阵的尺寸,可以从前往后看,比如:输入层是2个特征,输出层是3个神经元,则W的尺寸就是 2\times 3。
B的尺寸是1x3,列数永远和神经元的数量一样,行数永远是1。
输出层⚓︎
输出层三个神经元,再加上一个Softmax计算,最后有A1,A2,A3三个输出,写作:
其中,Z=X \cdot W+B,A = Softmax(Z)
7.2.2 样本数据⚓︎
使用SimpleDataReader类读取数据后,观察一下数据的基本属性:
reader.XRaw.shape
(140, 2)
reader.XRaw.min()
0.058152279749505986
reader.XRaw.max()
9.925126526921046
reader.YRaw.shape
(140, 1)
reader.YRaw.min()
1.0
reader.YRaw.max()
3.0
- 训练数据X,140个记录,两个特征,最小值0.058,最大值9.925
- 标签数据Y,140个记录,一个分类值,取值范围是\\{1,2,3\\}
样本标签数据⚓︎
一般来说,在标记样本时,我们会用1,2,3这样的标记来指明是哪一类。所以样本数据是这个样子的: $$ Y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_{140} \end{pmatrix}= \begin{pmatrix}3 \\ 2 \\ \vdots \\ 1\end{pmatrix} $$
在有Softmax的多分类计算时,我们用下面这种等价的方式,俗称OneHot。 $$ Y = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_{140} \end{pmatrix}= \begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ ... & ... & ... \\ 1 & 0 & 0 \end{pmatrix} $$
OneHot的意思,在这一列数据中,只有一个1,其它都是0。1所在的列数就是这个样本的分类类别。标签数据对应到每个样本数据上,列对齐,只有(1,0,0),(0,1,0),(0,0,1)三种可能,分别表示第一类、第二类和第三类。
在SimpleDataReader中实现ToOneHot()方法,把原始标签转变成One-Hot编码:
class SimpleDataReader(object):
def ToOneHot(self, num_category, base=0):
......
7.2.3 代码实现⚓︎
绝大部分代码可以从上一章的HelperClass中拷贝出来,但是需要我们为了本章的特殊需要稍加修改。
添加分类函数⚓︎
在Activators.py中,增加Softmax的实现,并添加单元测试。
class Softmax(object):
def forward(self, z):
......
前向计算⚓︎
前向计算需要增加分类函数调用:
class NeuralNet(object):
def forwardBatch(self, batch_x):
Z = np.dot(batch_x, self.W) + self.B
if self.params.net_type == NetType.BinaryClassifier:
A = Logistic().forward(Z)
return A
elif self.params.net_type == NetType.MultipleClassifier:
A = Softmax().forward(Z)
return A
else:
return Z
反向传播⚓︎
在多分类函数一节详细介绍了反向传播的推导过程,推导的结果很令人惊喜,就是一个简单的减法,与前面学习的拟合、二分类的算法结果都一样。
class NeuralNet(object):
def backwardBatch(self, batch_x, batch_y, batch_a):
......
计算损失函数值⚓︎
损失函数不再是均方差和二分类交叉熵了,而是交叉熵函数对于多分类的形式,并且添加条件分支来判断只在网络类型为多分类时调用此损失函数。
class LossFunction(object):
# fcFunc: feed forward calculation
def CheckLoss(self, A, Y):
m = Y.shape[0]
if self.net_type == NetType.Fitting:
loss = self.MSE(A, Y, m)
elif self.net_type == NetType.BinaryClassifier:
loss = self.CE2(A, Y, m)
elif self.net_type == NetType.MultipleClassifier:
loss = self.CE3(A, Y, m)
#end if
return loss
# end def
# for multiple classifier
def CE3(self, A, Y, count):
......
推理函数⚓︎
def inference(net, reader):
xt_raw = np.array([5,1,7,6,5,6,2,7]).reshape(4,2)
xt = reader.NormalizePredicateData(xt_raw)
output = net.inference(xt)
r = np.argmax(output, axis=1)+1
print("output=", output)
print("r=", r)
函数np.argmax的作用是比较output里面的几个数据的值,返回最大的那个数据的行数或者列数,0-based。比如output=(1.02,-3,2.2)时,会返回2,因为2.2最大,所以我们再加1,把返回值变成1,2,3的其中一个。
np.argmax函数的参数axis=1,是因为有4个样本参与预测,所以需要在第二维上区分开来,分别计算每个样本的argmax值。
主程序⚓︎
if __name__ == '__main__':
num_category = 3
......
num_input = 2
params = HyperParameters(num_input, num_category, eta=0.1, max_epoch=100, batch_size=10, eps=1e-3, net_type=NetType.MultipleClassifier)
......
7.2.4 运行结果⚓︎
损失函数历史记录⚓︎
从图7-8所示的趋势上来看,损失函数值还有进一步下降的可能,以提高模型精度。有兴趣的读者可以多训练几轮,看看效果。
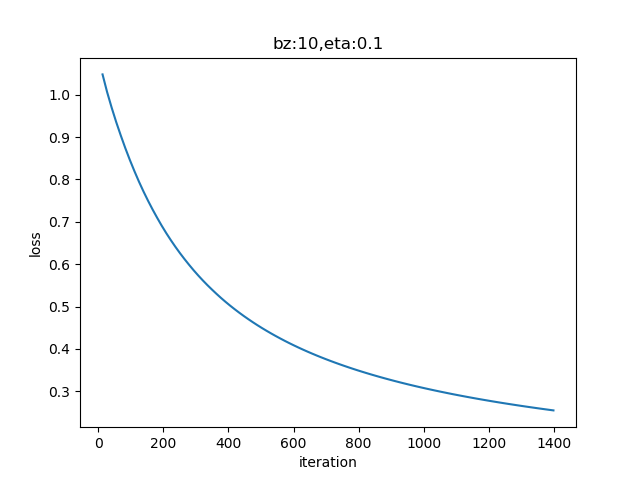
图7-8 训练过程中损失函数值的变化
下面是打印输出的最后几行:
......
epoch=99
99 13 0.25497053433985734
W= [[-1.43234109 -3.57409342 5.00643451]
[ 4.47791288 -2.88936887 -1.58854401]]
B= [[-1.81896724 3.66606162 -1.84709438]]
output= [[0.01801124 0.73435241 0.24763634]
[0.24709055 0.15438074 0.59852871]
[0.38304995 0.37347646 0.24347359]
[0.51360269 0.46266935 0.02372795]]
r= [2 3 1 1]
- 经纬度相对值为 (5,1) 时,概率0.734最大,属于2,蜀国
- 经纬度相对值为 (7,6) 时,概率0.598最大,属于3,吴国
- 经纬度相对值为 (5,6) 时,概率0.383最大,属于1,魏国
- 经纬度相对值为 (2,7) 时,概率0.513最大,属于1,魏国
代码位置⚓︎
ch07, Level1
思考与练习⚓︎
- 从4个样本的推理结果来看,分类都是正确的,但是只有第一个样本的结果的0.734的概率值处于绝对领先位置,其它几个分类的概率值优势并不明显,这是为什么?如何让其正确分类的概率值的差距更大?