07.1 多分类函数
7.1 多分类函数⚓︎
此函数对线性多分类和非线性多分类都适用。
先回忆一下二分类问题,在线性计算后,使用了Logistic函数计算样本的概率值,从而把样本分成了正负两类。那么对于多分类问题,应该使用什么方法来计算样本属于各个类别的概率值呢?又是如何作用到反向传播过程中的呢?我们这一节主要研究这个问题。
7.1.1 多分类函数定义 - Softmax⚓︎
如何得到多分类问题的分类结果概率值?⚓︎
Logistic函数可以得到诸如0.8、0.3这样的二分类概率值,前者接近1,后者接近0。那么多分类问题如何得到类似的概率值呢?
我们依然假设对于一个样本的分类值是用这个线性公式得到的:
但是,我们要求 z 不是一个标量,而是一个向量。如果是三分类问题,我们就要求 z 是一个三维的向量,向量中的每个单元的元素值代表该样本分别属于三个分类的值,这样不就可以了吗?
具体的说,假设x是一个 (1x2) 的向量,把w设计成一个(2x3)的向量,b设计成(1x3)的向量,则z就是一个(1x3)的向量。我们假设z的计算结果是[3,1,-3],这三个值分别代表了样本x在三个分类中的数值,下面我们把它转换成概率值。
有的读者可能会有疑问:我们不能训练神经网络让它的z值直接变成概率形式吗?答案是否定的,因为z值是经过线性计算得到的,线性计算能力有限,无法有效地直接变成概率值。
取max值⚓︎
z值是 [3,1,-3],如果取max操作会变成 [1,0,0],这符合我们的分类需要,即三者相加为1,并且认为该样本属于第一类。但是有两个不足:
- 分类结果是 [1,0,0],只保留的非0即1的信息,没有各元素之间相差多少的信息,可以理解是“Hard Max”;
- max操作本身不可导,无法用在反向传播中。
引入Softmax⚓︎
Softmax加了个"soft"来模拟max的行为,但同时又保留了相对大小的信息。
上式中:
- z_j 是对第 j 项的分类原始值,即矩阵运算的结果
- z_i 是参与分类计算的每个类别的原始值
- m 是总分类数
- a_j 是对第 j 项的计算结果
假设 j=1,m=3,上式为:
用图7-5来形象地说明这个过程。
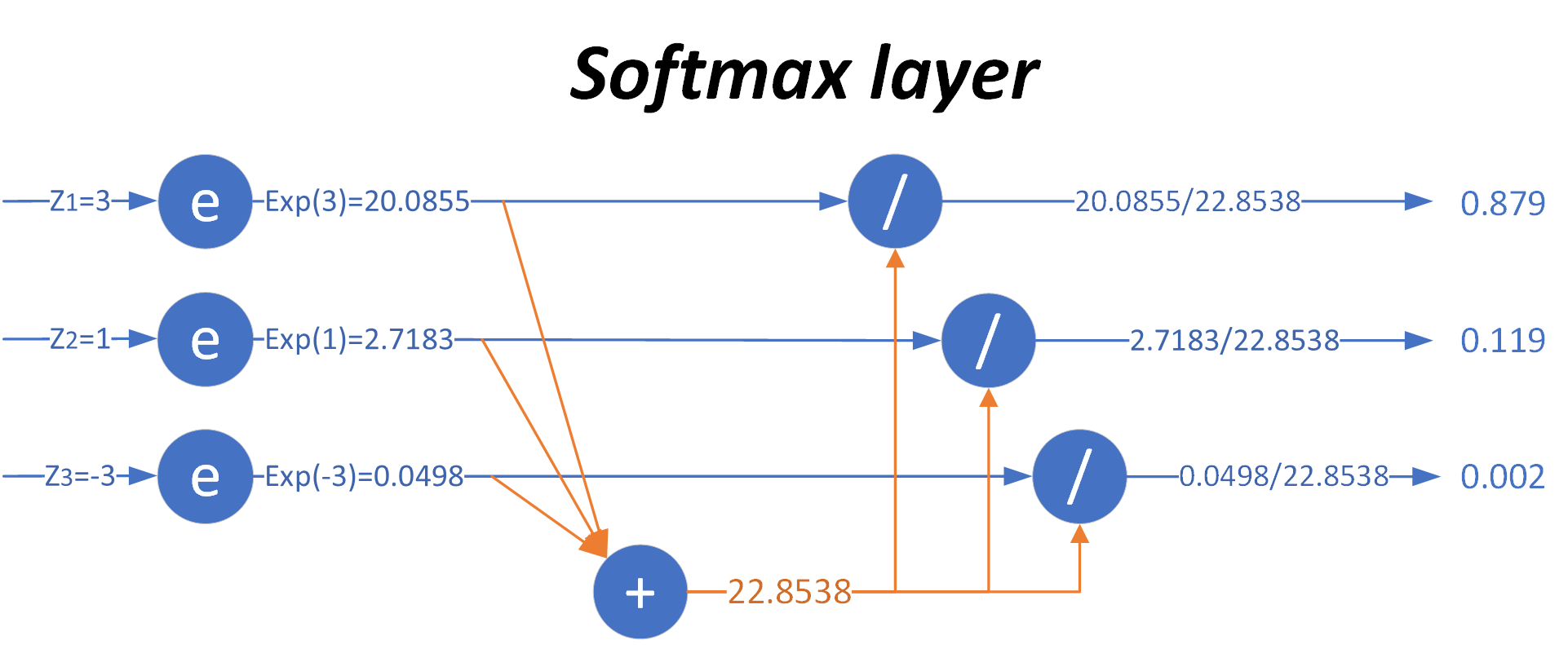
图7-5 Softmax工作过程
当输入的数据[z_1,z_2,z_3]是[3,1,-3]时,按照图示过程进行计算,可以得出输出的概率分布是[0.879,0.119,0.002]。
对比MAX运算和Softmax的不同,如表7-2所示。
表7-2 MAX运算和Softmax的不同
| 输入原始值 | MAX计算 | Softmax计算 |
|---|---|---|
| [3, 1, -3] | [1, 0, 0] | [0.879, 0.119, 0.002] |
也就是说,在(至少)有三个类别时,通过使用Softmax公式计算它们的输出,比较相对大小后,得出该样本属于第一类,因为第一类的值为0.879,在三者中最大。注意这是对一个样本的计算得出的数值,而不是三个样本,亦即Softmax给出了某个样本分别属于三个类别的概率。
它有两个特点:
- 三个类别的概率相加为1
- 每个类别的概率都大于0
Softmax的反向传播工作原理⚓︎
我们仍假设网络输出的预测数据是 z=[3,1,-3],而标签值是 y=[1,0,0]。在做反向传播时,根据前面的经验,我们会用 z-y,得到:
这个信息很奇怪:
- 第一项是2,我们已经预测准确了此样本属于第一类,但是反向误差的值是2,即惩罚值是2
- 第二项是1,惩罚值是1,预测对了,仍有惩罚值
- 第三项是-3,惩罚值是-3,意为着奖励值是3,明明预测错误了却给了奖励
所以,如果不使用Softmax这种机制,会存在有个问题:
- z值和y值之间,即预测值和标签值之间不可比,比如 z_0=3 与 y_0=1 是不可比的
- z值中的三个元素之间虽然可比,但只能比大小,不能比差值,比如 z_0>z_1>z_2,但3和1相差2,1和-3相差4,这些差值是无意义的
在使用Softmax之后,我们得到的值是 a=[0.879,0.119,0.002],用 a-y:
再来分析这个信息:
- 第一项-0.121是奖励给该类别0.121,因为它做对了,但是可以让这个概率值更大,最好是1
- 第二项0.119是惩罚,因为它试图给第二类0.119的概率,所以需要这个概率值更小,最好是0
- 第三项0.002是惩罚,因为它试图给第三类0.002的概率,所以需要这个概率值更小,最好是0
这个信息是完全正确的,可以用于反向传播。Softmax先做了归一化,把输出值归一到[0,1]之间,这样就可以与标签值的0或1去比较,并且知道惩罚或奖励的幅度。
从继承关系的角度来说,Softmax函数可以视作Logistic函数扩展,比如一个二分类问题:
是不是和Logistic函数形式非常像?其实Logistic函数也是给出了当前样本的一个概率值,只不过是依靠偏近0或偏近1来判断属于正类还是负类。
7.1.2 正向传播⚓︎
矩阵运算⚓︎
分类计算⚓︎
损失函数计算⚓︎
计算单样本时,m是分类数: $$ loss(w,b)=-\sum_{i=1}^m y_i \ln a_i \tag{3} $$
计算多样本时,m是分类数,n是样本数: J(w,b) =- \sum_{j=1}^n \sum_{i=1}^m y_{ji} \log a_{ji} \tag{4}
如图7-6示意。
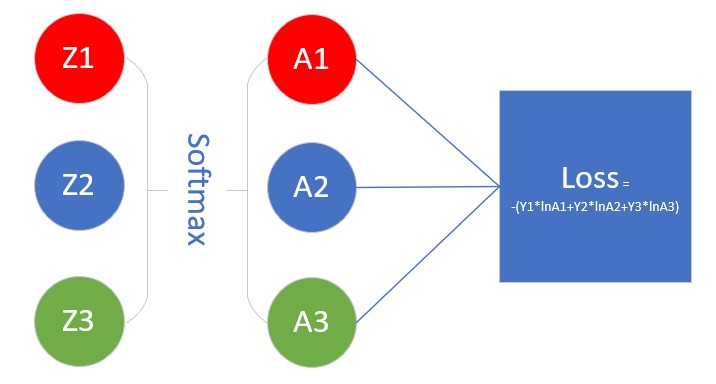
图7-6 Softmax在神经网络结构中的示意图
7.1.3 反向传播⚓︎
实例化推导⚓︎
我们先用实例化的方式来做反向传播公式的推导,然后再扩展到一般性上。假设有三个类别,则:
为了方便书写,我们令:
依次求解公式12中的各项:
把公式13~18组合到12中:
不失一般性,由公式19可得: $$ \frac{\partial loss}{\partial z_i}=a_i-y_i \tag{20} $$
一般性推导⚓︎
- Softmax函数自身的求导
由于Softmax涉及到求和,所以有两种情况:
- 求输出项 a_1 对输入项 z_1 的导数,此时:j=1, i=1, i=j,可以扩展到 i,j 为任意相等值
- 求输出项 a_2 或 a_3 对输入项 z_1 的导数,此时:j 为 2 或 3, i=1,i \neq j,可以扩展到 i,j 为任意不等值
Softmax函数的分子:因为是计算 a_j,所以分子是 e^{z_j}。
Softmax函数的分母: $$ \sum\limits_{i=1}^m e^{z_i} = e^{z_1} + \dots + e^{z_j} + \dots +e^{z_m} \Rightarrow E $$
- i=j时(比如输出分类值 a_1 对 z_1 的求导),求 a_j 对 z_i 的导数,此时分子上的 e^{z_j} 要参与求导。参考基本数学导数公式33:
- i \neq j时(比如输出分类值 a_1 对 z_2 的求导,j=1,i=2),a_j对z_i的导数,分子上的 z_j 与 i 没有关系,求导为0,分母的求和项中e^{z_i}要参与求导。同样是公式33,因为分子e^{z_j}对e^{z_i}求导的结果是0:
- 结合损失函数的整体反向传播公式
看上图,我们要求Loss值对Z1的偏导数。和以前的Logistic函数不同,那个函数是一个 z 对应一个 a,所以反向关系也是一对一。而在这里,a_1 的计算是有 z_1,z_2,z_3 参与的,a_2 的计算也是有 z_1,z_2,z_3 参与的,即所有 a 的计算都与前一层的 z 有关,所以考虑反向时也会比较复杂。
先从Loss的公式看,loss=-(y_1lna_1+y_2lna_2+y_3lna_3),a_1 肯定与 z_1 有关,那么 a_2,a_3 是否与 z_1 有关呢?
再从Softmax函数的形式来看:
无论是 a_1,a_2,a_3,都是与 z_1 相关的,而不是一对一的关系,所以,想求Loss对Z1的偏导,必须把Loss->A1->Z1, Loss->A2->Z1,Loss->A3->Z1,这三条路的结果加起来。于是有了如下公式:
当上式中i=1,j=3,就完全符合我们的假设了,而且不失普遍性。
前面说过了,因为Softmax涉及到各项求和,A的分类结果和Y的标签值分类是否一致,所以需要分情况讨论:
因此,\frac{\partial{loss}}{\partial{z_i}}应该是 i=j 和 i \neq j两种情况的和:
- i = j 时,loss通过 a_1 对 z_1 求导(或者是通过 a_2 对 z_2 求导):
- i \neq j,loss通过 a_2+a_3 对 z_1 求导:
把两种情况加起来:
因为y_j取值[1,0,0]或者[0,1,0]或者[0,0,1],这三者加起来,就是[1,1,1],在矩阵乘法运算里乘以[1,1,1]相当于什么都不做,就等于原值。
我们惊奇地发现,最后的反向计算过程就是:a_i-y_i,假设当前样本的a_i=[0.879, 0.119, 0.002],而y_i=[0, 1, 0],则: a_i - y_i = [0.879, 0.119, 0.002]-[0,1,0]=[0.879,-0.881,0.002]
其含义是,样本预测第一类,但实际是第二类,所以给第一类0.879的惩罚值,给第二类0.881的奖励,给第三类0.002的惩罚,并反向传播给神经网络。
后面对 z=wx+b 的求导,与二分类一样,不再赘述。
7.1.4 代码实现⚓︎
第一种,直截了当按照公式写:
def Softmax1(x):
e_x = np.exp(x)
v = np.exp(x) / np.sum(e_x)
return v
np.exp(x)很容易溢出,因为是指数运算。所以,有了下面这种改进的代码:
def Softmax2(Z):
shift_Z = Z - np.max(Z)
exp_Z = np.exp(shift_Z)
A = exp_Z / np.sum(exp_Z)
return A
Z = np.array([3,0,-3])
print(Softmax1(Z))
print(Softmax2(Z))
[0.95033021 0.04731416 0.00235563]
[0.95033021 0.04731416 0.00235563]
为什么一样呢?从代码上看差好多啊!我们来证明一下:
假设有3个值a,b,c,并且a在三个数中最大,则b所占的Softmax比重应该这样写:
如果减去最大值变成了a-a,b-a,c-a,则b'所占的Softmax比重应该这样写:
Softmax2的写法对一个一维的向量或者数组是没问题的,如果遇到Z是个M \times N维(M,N>1)的矩阵的话,就有问题了,因为np.sum(exp_Z)这个函数,会把M\times N矩阵里的所有元素加在一起,得到一个标量值,而不是相关列元素加在一起。
所以应该这么写:
class Softmax(object):
def forward(self, z):
shift_z = z - np.max(z, axis=1, keepdims=True)
exp_z = np.exp(shift_z)
a = exp_z / np.sum(exp_z, axis=1, keepdims=True)
return a
axis=1这个参数非常重要,因为如果输入Z是单样本的预测值话,如果是分三类,则应该是个 3\times 1 的数组,如果:
- z = [3,1,-3]
- a = [0.879,0.119,0.002]
但是,如果是批量训练,假设每次用两个样本,则:
if __name__ == '__main__':
z = np.array([[3,1,-3],[1,-3,3]]).reshape(2,3)
a = Softmax().forward(z)
print(a)
[[0.87887824 0.11894324 0.00217852]
[0.11894324 0.00217852 0.87887824]]
如果s = np.sum(exp_z),不指定axis=1参数,则:
[[0.43943912 0.05947162 0.00108926]
[0.05947162 0.00108926 0.43943912]]
思考与练习⚓︎
- 有没有可能一个样本的三分类值中,有两个或多个分类值相同呢,比如[0.3,0.3,0.4]?
- 遇到这种问题是你打算如何解决?